An improved multiphase SPH algorithm with kernel gradient correction for modelling fuel–coolant interaction

1 Introduction

As the most mature reactor of Generation-IV advanced reactor systems, a sodium-cooled fast reactor (SFR) has advantages such as good inherent safety, high breeding ratio, high thermal conductivity, and long-life radioactive waste transmutation. Rich experience with operating systems laid the foundation of its commercialization. However, once the anticipated transients without scram, including unprotected transient overpower and unprotected loss of flow, happened, the boiling coolant could cause an increase in reactivity, exacerbating the consequences and leading to core disruption and fuel melting (Tobita et al., 2016). Although the probability of core disruptive accident (CDA) is very low, it is crucial for reactor safety assessment. Molten fuel ejected from the cladding rupture is mixed with the coolant and forms fragments. The behavior and size of fuel fragments formed in the fuel–coolant interaction (FCI) significantly affect the heat transfer deterioration in core as well as cooling and re-criticality in the lower head and core catcher (Cheng et al., 2019).

From this point of view, a number of experimental research studies have been conducted on the FCI related to an SFR to figure out the fragmentation characteristics over the past decades (Iwasawa and Abe, 2018). Some researchers used molten fuel materials (U/UO₂) in pursuit of a realistic core condition. Armstrong reported a series of experiments about the interactions between UO₂/stainless steel and liquid sodium in a dropping mode (Armstrong 1971) (Armstrong et al., 1976). Gabor et al. (1988) performed experiments by pouring molten metallic fuel and its alloy in quantities of kilogram into a sodium pool and focused on breakup behaviors. In most of the later experiments, as core materials are not readily available, materials with physical properties similar to fuel, such as copper, were often used as substitutes (Schins and Gunnerson, 1986; Nishimura et al., 2007; Nishimura et al., 2010; Zhang and Sugiyama, 2012). The fragmentation mechanisms are usually inferred based on the size and morphology of the solid fragments. Nishimura et al. (2010) carried out the FCI experiment in the form of a single molten copper jet penetrating into a sodium pool and analyzed the fragmentation characteristics from hydraulic and thermal perspectives. The processes of a single molten copper droplet (Nishimura et al., 2007; Zhang et al., 2009; Zhang and Sugiyama, 2010; Zhang and Sugiyama, 2012) and continuous copper droplets (Yang et al., 2018; Yang et al., 2019) interacting with liquid sodium have also been studied, and a thermal fragmentation mechanism of sodium entrainment was proposed and fragmentation due to a sodium microjet was presented.

In order to get rid of the limitation of core materials and obtain a visible development process, some scholars chose numerical methods to study the FCI. Cheng et al. (2015b) used SIMMER-III, which is a safety analysis code characterized by multivelocity field, multiphase, and multicomponent modeling to simulate the experimental tests of fuel–water interaction conducted at the Japan Atomic Energy Agency (Cheng et al., 2015a), to figure out the characteristics including pressure buildup and mechanical energy release. Because the FCI is a complex phenomenon involving multiphase flow, intense interfacial motion, drastic heat transfer, and phase transitions, it is challenging for traditional grid methods to capture these details, and some technical limitations emerge, such as grid distortion in the Lagrange grid method or difficult interface tracking in the Euler grid method when dealing with such large deformation multiphase flow problems. Therefore, some scholars have turned to meshfree methods, which have received extensive attention in recent years. The computational domain of the particle method is represented by a series of randomly distributed particles carrying material properties. Due to these moving Lagrange particles, the meshfree particle methods obtain attractive features and inherent advantages in solving complex hydrodynamics problems. The moving particle semi-implicit (MPS) method and smoothed particle hydrodynamics (SPH) are two typical meshfree particle methods. MPS was first proposed by Koshizuka and Oka (1996) and focused on thermal–hydraulic simulations in nuclear field. Abundant models related to incompressible flow have been developed in the MPS framework for calculating surface tension, heat conduction and convection, open inlet and outlet boundaries, fluid–structure interaction, and other problems. The development and application of MPS in nuclear engineering are well-reviewed by Li et al. (2020). SPH is the first meshfree particle method proposed by Lucy (1977) and Gingold and Monaghan (1977). With sufficient development, it has been widely used in marine, aerospace, and other fields covering compressible, weakly compressible, and incompressible flows (Lind et al., 2020). The fundamental difference between MPS and SPH lies in the solution of pressure. The pressure of incompressible flow in MPS is calculated by implicitly solving the pressure Poisson equation, which requires solving a super large-scale matrix. It is a severe test of computational cost and parallel feasibility, especially with a huge number of particles (Li et al., 2020). Considering the large-scale particle computation and parallel algorithms are the general trend, although SPH is rarely used in nuclear field compared with MPS, SPH is chosen in this paper for its development potential with explicit solution, which makes it easy to improve the computational efficiency through parallelism. In order to handle the density discontinuity across the multiphase interface, a few solutions have been proposed. In this paper, one of the popular ideas based on particle number density is adopted (Hu and Adams, 2006; Hu and Adams, 2007; Szewc et al., 2015). However, there are still errors under this approximation idea, and the accumulated errors lead to the situation where the stability and accuracy of the calculation cannot be maintained for a long time. Therefore, this study introduced kernel gradient correction (KGC) and combined it with the use of particle number density. The significantly better performance of the improved method in dealing with multiphase flow has been demonstrated and emphasized. The multiphase SPH corrected with KGC is abbreviated as KGC-MSPH in this paper. The program in this paper is developed based on FORTRAN language and uses OpenMP to realize parallel computation.

This paper is organized as follows: in the second section, the basic physical models, namely, conservation equations and equations of state, are introduced. Then, the third section describes the numerical scheme, including the basic principle of SPH and models and corrections used in multiphase SPH. In the fourth section, the numerical investigation of KGC-MSPH is explained with the test cases. Finally, we apply the validated method to the simplified FCI condition and discuss the simulation results.

2 Physical models

The Navier–Stokes equations used to describe the flow system in a Lagrangian frame are applied. The continuity equation and the momentum equation are as follows:

where $\rho$ is the density, $\mathit{v}$ is the velocity vector, $p$ is the pressure, and $t$ is the time. The pressure gradient $-\nabla p$, viscous stress ${\mathit{f}}_{\mathit{v}}$, surface tension force ${\mathit{f}}_s$, and the gravity $\mathit{g}$ are contained in the momentum equation. In the SPH framework, the incompressible fluids are usually assumed to be weakly compressible. Thus, the pressure is directly related to the density and can be calculated explicitly via the equation of state. Here, the commonly used Tait equation (Monaghan, 1994) is applied,

where, $c_0$ is the artificial sound speed. The value of $c_0$ determines the compressibility of the fluid and it must be ten times greater than the maximum value of the fluid velocity to satisfy the weakly compressibility hypothesis (Monaghan and Kos, 1999). For single-phase flow and the denser phase in multiphase flow, $\gamma$ is usually set to be $7$, and it takes a smaller value for the lighter phase, which is usually $1.4$ under the large density ratio of water to air (Colagrossi and Landrini, 2003; Grenier et al., 2009). The relation of the artificial sound speeds for different phases, phase $X$ and phase $Y$, satisfies the condition ${\rho }_{0,X}{c_{0,X}}^2/{\gamma }_X={\rho }_{0,Y}{c_{0,Y}}^2/{\gamma }_Y$. $p_b$ is the background pressure. It has a positive value for the multiphase flow to avoid negative pressures. The application of background pressure is beneficial to the uniformity of particle distribution and the stability of calculation (Marrone et al., 2013; Zhang et al., 2015).

3 Numerical scheme

3.1 Basic principle of SPH

In SPH, the computational domain is represented by a finite number of particles, which carry physical properties like real fluid elements. A kernel function is applied to establish the relationship between particles. The kernel approximation works by integrating over the surrounding particles to express the central one. The arbitrary function $A\left(\mathit{x}\right)$ at a general position $\mathit{x}$ in the domain $\Omega$ and its derivative in SPH form are obtained,

where, $W\left(\mathit{x}-{\mathit{x}}^{\prime },h\right)$ is the smoothing kernel function. The support domain of the kernel function is measured by the smoothing length $h$ and it is discretized into $N$ particles. When $h$ becomes 0, $W\left(\mathit{x}-{\mathit{x}}^{\prime },h\right)$ has the characteristic of the Dirac function and the kernel integral over the support domain is equal to 1. The subscript $j$ is used to label the variables of these adjacent particles, like the mass $m_j$ and the density ${\rho }_j$. All the particles in the computational domain can be expressed by contributing to each other in the summations.

The kernel function plays an important role in the SPH simulation and significantly affects the numerical results. Here, we consider two kernel functions. One is the renormalized Gaussian kernel (Grenier et al., 2009; Molteni and Colagrossi, 2009) used in the deformation of square droplet, given as follows:

where, $r=\left|{\mathit{x}}_i-{\mathit{x}}_j\right|$ is the distance between two particles, $q=r/h$ and $C_0=e^{-9}$ and $C_1=10C_0$. The cut-off radius is set to be $3h$.

The other one is the Wendland kernel (Dehnen and Aly, 2012; Ferrand et al., 2013) used in the other cases, given as

where, the cut-off radius is set to be $2h$.

3.2 MSPH formulations

The density estimation is the basis in the SPH frame and is achieved either by the continuity equation or by the density summation approach. In order to handle the density discontinuity across the multiphase interface, a few variants of density estimation have been developed. The special volume proposed by Hu and Adams (2006) is used in the present work. It is based on the density summation theory with the use of an interpolating function, given as

where, $W_j\left({\mathit{x}}_i\right)$ is the abbreviation of $W_j\left({\mathit{x}}_i-{\mathit{x}}_j,h\right)$. $\sigma \left({\mathit{x}}_i\right)$ is the particle density number. The special volume calculated with the interpolating function is as follows:

After the aforementioned derivation, the special volume $V_i^{\sigma }$ is the inverse of ${\sigma }_i$, which only requires the position information of the adjacent particles. With the mass of particle $i$ known as a constant, the density can be approximated as,

The density of particle $i$ is not influenced by the mass or density of the neighbors, and this multiphase model is able to reproduce the discontinuous density field.

Based on the multiphase SPH idea, the momentum conservation equation Eq. 2 can be discretized as,

The acceleration term driven by the pressure gradient in Eq. 11 has the anti-symmetric form, which is variationally consistent with the form of density estimation.

In addition to density, some other physical properties are discontinuous across the multiphase interface, such as viscosity. To deal with the viscosity jump, the viscous coefficient is calculated in a harmonic mean form proposed by Hu and Adams (2006). The formula of the viscous force ${\mathit{f}}_{v,i}$ is given as,

where, $\eta$ is the dynamic viscous coefficient and $\xi$ is a small constant, usually taken to be 0.01, to prevent the denominator from being 0 when two particles coincide.

Here, the surface tension force is calculated using the CSF model (Brackbill et al., 1992) in the form ${\mathit{f}}_s=-\alpha \kappa \mathit{n}\lambda$. $\alpha$ is the surface tension coefficient, $\kappa$ is the curvature of the interface, and $\mathit{n}$ is the unit normal vector. $\lambda$ is a weight function used to define a transition zone near the interface and determine the magnitude of the surface tension across the zone. The calculation of $\mathit{n}$ and $\lambda$ requires a density-weighted color function $c$ such that $\mathit{n}=\nabla c/\left|\nabla c\right|$ and $\lambda =\left|\nabla c\right|$. The formulas are given as (Adami et al., 2010)

where, $c_i^j$ represents the relationship between particle $i$ and the neighbor particle $j$, $S$ is the phase to which particle $i$ belongs to, and $c_{i,W}^j$ is the density-weighted color function. The SPH approximation of the unit normal vector is obtained as,

The curvature $\kappa$ presented in Adami et al. (2010) using a reproducing divergence is applied here. The benefit of this reproducing divergence is that the support domain truncated condition can be handled more accurately. The curvature in the CSF model can be calculated as follows:

where, ${\varphi }_i^j$ is used to describe the direction of the unit vector by determining whether the particles $i$ and $j$ belong to the same phase and $d$ is the spatial dimension. Then, the surface tension force is obtained.

The good performance of this surface tension model in multiphase flow is demonstrated in this study by simulating the oscillatory deformation of a square droplet.

3.3 Time-stepping scheme

The time-stepping scheme is fully explicit. Similar to Zhang et al. (2015), a modified predictor-corrector time-stepping scheme is used in this paper to integrate Eqs 1, 2. The integration process is divided into two steps. The following equation gives the prediction step of the algorithm.

where, the subscripts $n$ and $n+1/2$ represent, respectively, the previous step and the prediction step. $∆t$ is the timestep which is determined by the CFL condition. The correction step, namely, the present $n+1$ step is updated as,

3.4 Solid boundary treatment

In this paper, the solid boundary condition is carefully set with ghost particles, which have a mirroring relationship with the fluid particles within $3h$ of the boundary. Here, we use the lower subscripts $g$, $f$, $\mathrm{a}\mathrm{n}\mathrm{d}w$ to mark the information of the ghost particles, fluid particles, and the wall, respectively. The subscripts $n$ and $t$, respectively, mean the normal and tangential direction. The position of the ghost particle is easy to obtain with the mirroring relation as ${\mathit{x}}_g={2\mathit{x}}_w-{\mathit{x}}_f$. The common conditions of regular boundaries are mainly divided into no-slip and slip. The boundary conditions are expressed by the tangential velocity with ${\mathit{v}}_{g,t}=-{\mathit{v}}_{f,t}$ for no-slip and ${\mathit{v}}_{g,t}={\mathit{v}}_{f,t}$ for slip condition. The normal velocity of ghost particles is opposite to that of liquid particles to prevent particles from penetrating the wall. In the case of intense flow, the opposite normal velocity is not enough to stop the particle penetration. Therefore, an additional repulsive force (Monaghan, 1994) is needed, and its formula is as follows:

where, the distance between the ghost particle and the fluid particle is calculated as $r_{gf}=\left|{\mathit{x}}_{i,g}-{\mathit{x}}_{j,f}\right|$. $r_w$ is the cut-off radius, and it is taken as the initial spacing. The two powers are set as $n_1=4$ and $n_2=2$. The value of $D$ is on the order of the square of the maximum velocity.

3.5 Kernel gradient correction

Kernel gradient correction was developed to improve the simulation accuracy, and Bonet and Lok (1999) proved that by theoretical derivation. Shao et al. (2012) and Zhang and Liu (2017) have applied KGC in SPH simulation of liquid sloshing dynamics, high velocity impact, and violent impinging flow problems (Shao et al., 2016), which all focus on single-phase flow problems. Zhu et al. (2018) presented a SPH model for simulating multiphase flows with the use of KGC. In their work, the density is evaluated by the continuity equation, and the interface sharpness was maintained by developing an interface treatment algorithm, which consists of a virtual particle technique and an interface force. Here, the density discontinuity is handled by calculating the special volume based on density summation idea. The introduction of KGC can significantly improve the multiphase SPH model in this work, and the solution procedure of KGC-MSPH is relatively simple. The remarkable performance of KGC will be discussed in the numerical cases. The KGC formulation can be derived as follows:

The corrected kernel gradient can be obtained by modifying the original gradient with a reversible matrix,

Since the $d\times d$ matrix is defined by the local particle information, a high computation cost is required, which is a drawback.

3.6 The interfacial repulsive force

The interfacial repulsive force is commonly used in multiphase SPH-related studies (Monaghan, 2000; Grenier et al., 2009). If surface tension force is not considered, a spurious fragmentation can happen on the interface. The application of interfacial repulsive force can maintain the interface sharpness. This repulsive force is added to the pressure term depending on different situations and requirements. The discretized momentum equation considering the interfacial repulsive force can be written as follows:

The interfacial repulsive force only appears near the interface and vanishes if the neighbor particles belong to the same phase. The effect of the interfacial repulsive force is negligible on the surface tension force, and the magnitude of the force is determined by the coefficient $\epsilon$, where $\epsilon$ is generally less than $0.1$ (Grenier et al., 2009; Monaghan and Rafiee, 2013). We introduced the interfacial repulsive force in this study and discussed the coefficient value applicable to our method.

4 Numerical investigations

4.1 Deformation of square droplet

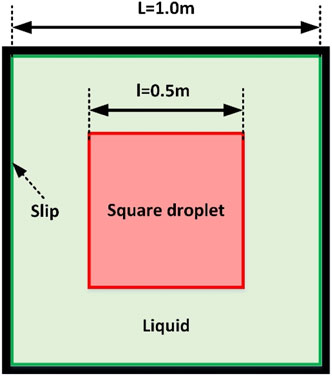
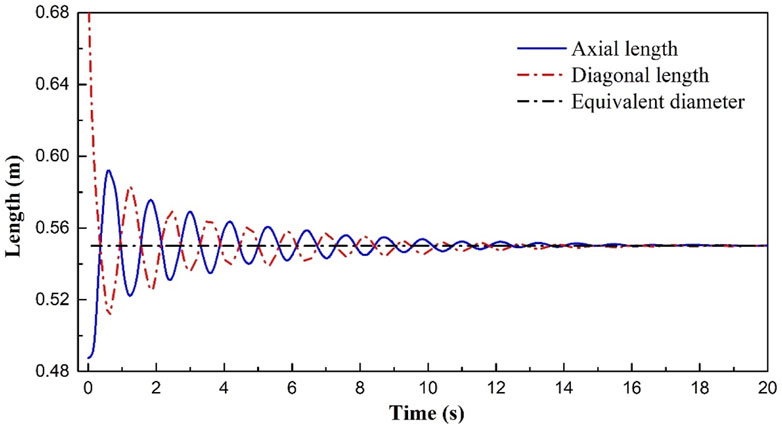
In this section, the KGC-MSPH method is analyzed and verified by a 2D simulation of the deformation of a square droplet. This case has been studied by Ming et al. (2017), and Patiño-Nariño et al. (2019) simulated a simple case of a circle drop resettling under a zero gravity condition. The multiphase SPH models adopted in their work are also based on calculations of particle number density and specific volumes. Distorted and mixed-interface problem plagued them. In order to maintain the sharpness under the high density ratio and suppress the instabilities, some treatments, like background pressure and interface sharpness control and inter-particle approximation of average pressure value, are applied in their simulations. Here, we use the same case to demonstrate the effectiveness of KGC on this problem and make comparative analysis with their treatments.

The initial condition is shown in Figure 1. A square droplet with side length $l$ = 0.5 $m$ is located in the center of a square cavity with side length $L$ = 1.0 $m$. The computational domain is discretized into 80 × 80 particles with uniform spacing $∆x$ = 0.0125 $m$. The timestep is set as $∆t={10}^{-4}s$. The wall boundary is simulated with the free-slip condition using mirror ghost particles without additional repulsive force. The liquid inside the droplet is marked with subscript $in$, and the subscript $out$ is used for marking the liquid outside the droplet in the cavity. The density ratio is defined as $\Psi ={\rho }_{in}/{\rho }_{out}$, and the viscosity ratio is $\Phi ={\eta }_{in}/{\eta }_{out}$. The density of the liquid inside and the dynamic viscous coefficient of the liquid outside are fixed as ${\rho }_{in}=$ 1000 $kg/m^3$ and ${\eta }_{out}=$ 0.2 $Pa\bullet s$, respectively. The prominent driven force, surface tension, is simulated with the density-weighted CSF model and $\alpha =$ 10.0 $N/m$. The background pressure is introduced here to prevent the tensile instability, and it is set as $P_b=$ 500 $Pa$.

FIGURE 1. Initial setup of square droplet deformation.

For comparison, the MSPH basic method without correction is used in this case where $\Psi =$ 1000 and $\Phi =1$. The same condition is simulated with KGC-MSPH. Under the action of surface tension, the square droplet oscillated periodically and gradually converged to a circular droplet. Several typical moments in the first oscillation period of droplet deformation simulated by MSPH and KGC-MSPH are shown in Figure 2. The first two figures on the top row indicate that, without correction, the results of MSPH calculation are reasonable at the initial stage of calculation. However, such a smooth interface cannot be maintained for a long time. As the calculation is performed, the problems of mixing and distortion breakage appear on the interface and gradually become worse. The problem is completely solved with the use of KGC. The interface is smooth, and the calculation is stable. The whole process of the droplet periodic oscillation and convergence into a circle has been simulated. The axial and diagonal size changes of the droplet during the deformation process are shown in Figure 3. The droplet had completed more than ten significant oscillation periods within 20 s, and the final axial and diagonal sizes converged to the analytical equivalent diameter. The theoretical value of the oscillation period is calculated $t_{period}=2\pi \sqrt{{\rho }_{in}{R}_a/60\alpha }=1.215s$, where $R_a$ is the analytic radius of the circle. The simulated oscillation period is in good agreement with $t_{period}$. We further increased the density ratio to 10000 and increased the range of viscosity ratio to 10–100. The total kinetic energy fluctuated with the oscillation in these conditions as shown in Figure 4. When $\Psi =$ 10000, KGC-MSPH is still competent for the simulation of deformation. Since the momentum of the external fluid is negligible for its small density, the variation of total kinetic energy is basically consistent with the curve of $\Psi =$ 1000. In the oscillation process of the square droplet with a high viscosity ratio, the kinetic energy is rapidly transformed into potential energy, the oscillation period is obviously reduced, and the droplet converged into a circle more rapidly. The results indicate that KGC-MSPH is capable of simulating the multiphase flow with a high density ratio and a high viscosity ratio. With KGC, a simple correction operation, stable and accurate results can be obtained in this case.

FIGURE 2. Comparison of square droplet oscillation simulated with MSPH and KGC-MSPH.

FIGURE 3. The variation of axial and diagonal sizes of the droplet.

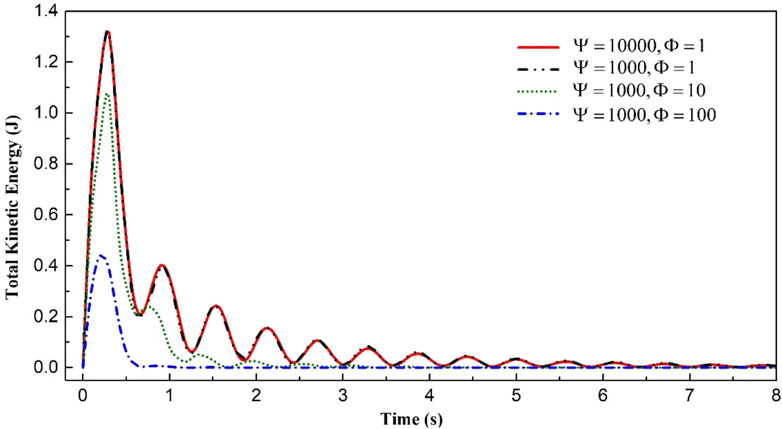
FIGURE 4. The variation of total kinetic energy of the droplet deformation with different density ratio and viscosity ratio.

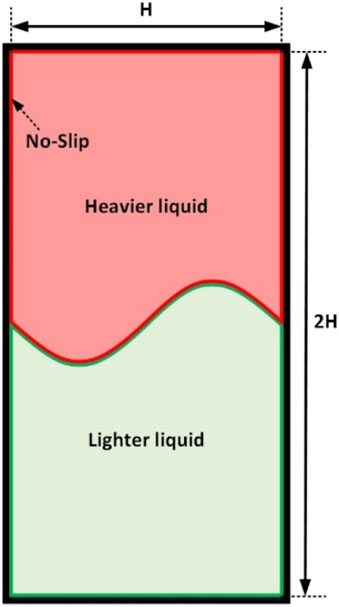
4.2 Rayleigh–Taylor instability

In order to further demonstrate the good performance of KGC-MSPH in gravity flow, we select a classic case, Rayleigh-Taylor (R–T) instability, which has been studied by Cummins and Rudman (1999), Grenier et al. (2009), and Hu and Adams (2009) in many ways. The computational domain is rectangular with size of 1.0 $m$ ×2.0 $m$ and is discretized into 150 × 300 particles. The timestep is set at $∆t={10}^{-4}s$. The heavier fluid in the upper layer with density ${\rho }_h=1800kg/m^3$ and the lighter fluid in the lower layer with density ${\rho }_l=1000kg/m^3$ are separated by the interface at $y=1.0-0.15\sin \left(2\pi x\right)$. The Reynolds number is set as $Re=\sqrt{H^{3}g}/\upsilon =420$, where $H=$ 1.0 $m$ and the gravity acceleration is $g=$ 1.0 $m/s^2$. The fluids have no initial velocity and begin to flow gradually driven by gravity. The boundary condition is set as no-slip, and no surface tension is considered here. The initial setup of this case is shown in Figure 5.

FIGURE 5. Initial setup of Rayleigh-Taylor instability.

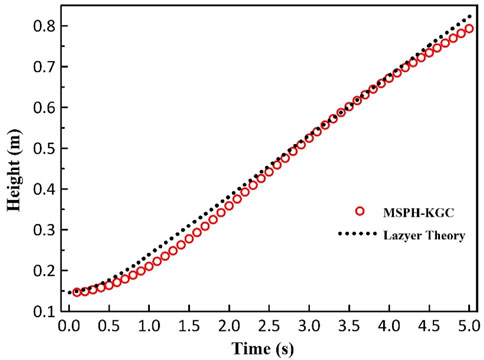
With KGC modification, MSPH is qualified for simulating R–T instability, and the contour of the interphase interface is well-described. The variation of the highest front position of the lighter fluid is in good agreement with the Layzer theory as shown in Figure 6. Because no external force is applied to the interface, slight unsmoothness occurred as shown in Figure 7A. The repulsive force model commonly used by scholars (Monaghan, 2000; Grenier et al., 2009; Monaghan and Rafiee, 2013) to stabilize multiphase interfaces was introduced. Snapshots of simulation results under repulsive forces of varying magnitude with $\epsilon =$ 0.01 and $\epsilon =$ 0.08, at $t=$ 0.5 $s$, are shown in Figures 7B, C, respectively. The smoothing effect of the repulsive force is clearly observed in the enlarged images. The interface is moderately smoothed with $\epsilon =$ 0.01. However, with $\epsilon =$ 0.08, the interface is overly smoothed and many details are erased, which is unreasonable. We suggest that in KGC-MSPH, the value should not be too large and preferably around 0.01 to avoid excessive influence on the interface.

FIGURE 6. The highest front position of a light fluid over time with ε = 0.01.

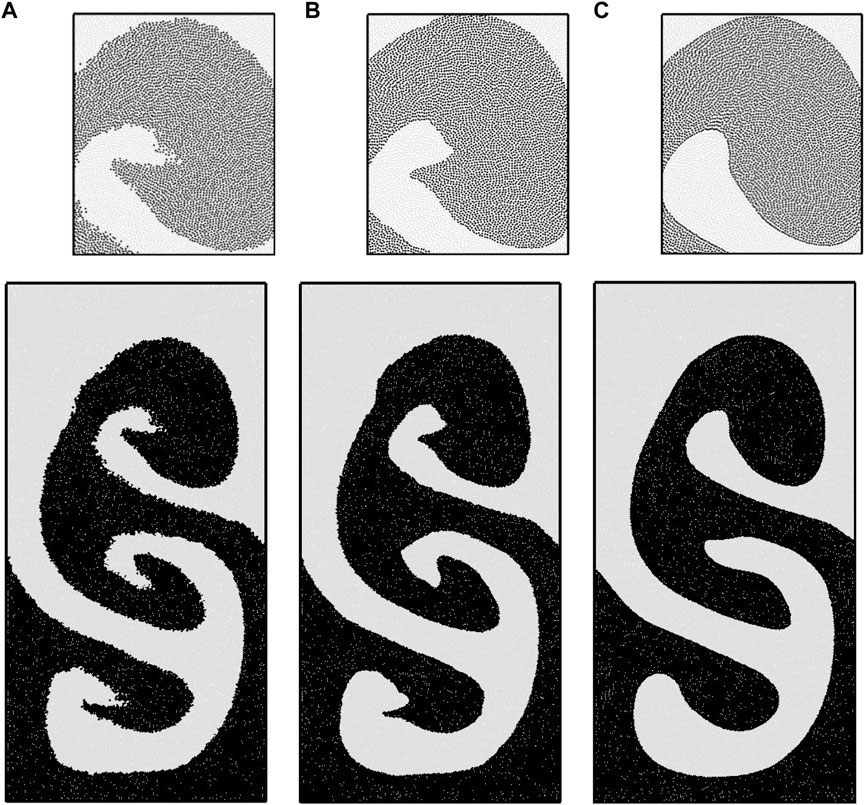
FIGURE 7. Snapshots of R-T instability at t = 5.0 s obtained by A MSPH-KGC, B MSPH-KGC with repulsive force ε = 0.01, C MSPH-KGC with repulsive force ε = 0.08.

We can conclude in this section that KGC-MSPH is capable of simulating R–T instability problem. The KGC correction fundamentally stabilizes the calculation and improves the calculation accuracy. If a smooth interface is desired, surface tension can be applied or an appropriate repulsive force can be introduced.

4.3 Bubble rising

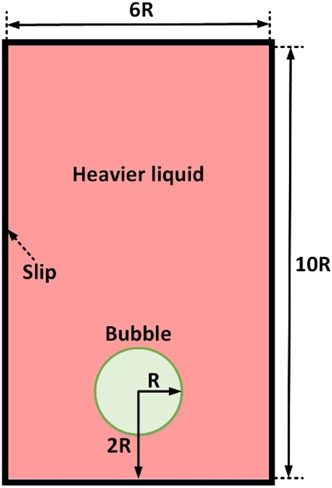
Bubble dynamics plays an important role in multiphase flow. The bubble rising problem has been studied with experiments, such as Collins (1967); Liu et al. (2016), and it has been extensively simulated, such as Sussman et al. (1994) with a level set method and Krishna et al. (2000) with a VOF method. As an important multiphase benchmark case, the bubble rising process is accompanied with interface deformation subjected to gravity force, viscosity, and surface tension, and it is a test to the algorithms. We applied KGC-MSPH to simulate the bubble rising process, and the results are compared to those in previous literature (Sussman et al., 1994) obtained with the level set method to prove the effectiveness of KGC-MSPH. The initial condition of this case is shown in Figure 8, and the bubble with radius $R=$ 1.0 $m$ rests in a rectangular container. The width of the container is $6R$ and the height $H=10R$. The center of the bubble is located on the axis of the container and $2R$ away from the bottom of the container. We use the subscript $m$ for referring to the bubble and $n$ for the heavier liquid outside. The densities are set as ${\rho }_m/{\rho }_n=1/1000$. The viscosity is defined by the Reynolds number $Re=\sqrt{\left({2R}^3\right)g}/{\upsilon }_n=1000$, where $\upsilon$ is the kinematic viscous coefficient and ${\upsilon }_m/{\upsilon }_n=128$. The surface tension is defined by the Bond number $Bond=4{\rho }_{n}g{R}^2/\alpha =200$. A small repulsive force is considered here with $\epsilon =0.01$. The background pressure is set to be $P_b=1000Pa$, and the artificial sound speeds of the two phases are, respectively, as $c_n=5\sqrt{gH}$ and $c_m=42.5\sqrt{gH}$.

FIGURE 8. Initial setup of bubble rising.

The timestep is set as $∆t={10}^{-5}s$. The computational domain is discretized into two resolutions, 192 × 320 and 384 × 640, and it is placed in a Cartesian coordinate system with the origin of the coordinates in the lower left corner. Those snapshots demonstrating typical shapes, including horseshoe-shaped, mushroom-shaped, daughter bubble formation, and detachment, are shown in Figure 9. In this condition, the bubble body is elongated and pinched off, forming the daughter bubbles. This process, which is tricky for the multiphase methods, is well-handled here. The evolutions under the two resolutions are almost consistent with each other, and the details in higher resolution are slightly better. It is further compared with the level set results, and good agreement can be observed.

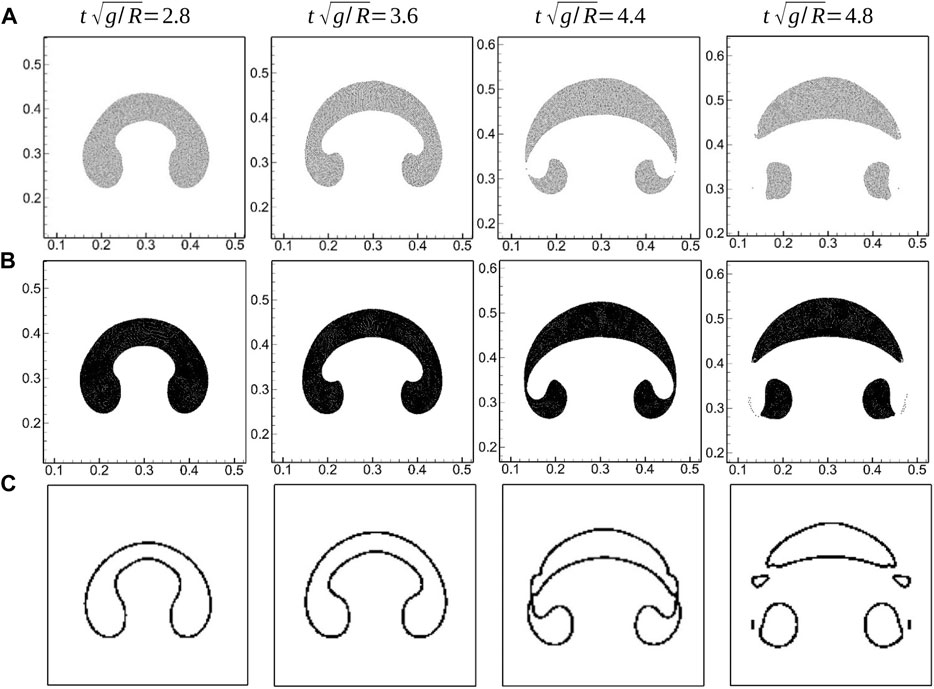
FIGURE 9. Snapshots of bubble rising. A MSPH-KGC solution with resolution of 192 × 320, B MSPH-KGC solution with resolution of 384 × 640, C Level set solution in (Sussman et al., 1994).

5 FCI simulation and mechanism analysis

Considering economy, safety, and reliability as well as engineering technology foundation, various countries have gradually agreed on the design scheme of the SFR. The core is made of metal fuel or MOX fuel, and stainless steel is used as the cladding material. Metal-fueled fast reactors are promising because metal fuels have better proliferative properties than MOX fuels, which is an important advantage for fast reactors (Carmack et al., 2009). However, metal uranium fuel has poor irradiation stability, low melting point, and is easy to crystallize with cladding at low temperature (Ogata, 2014). These shortcomings threaten the safety of the reactor core in serious accidents and may lead to CDAs. As an important phenomenon contained in CDAs (Tobita et al., 2016), molten fuel is fragmented and solidified into debris surrounding by the coolant in the FCI. The debris is relocated on the lower head or the core catcher. The fragmentation characteristics of the FCI significantly affect the heat transfer deterioration in core as well as cooling and re-criticality in the lower head and core catcher. The FCI is numerically studied with the developed KGC-MSPH method in this work. The fuel material is uranium, and the coolant is sodium. The interactions between the fuel, which is coated with melted cladding material, and the coolant were simulated as well. In practice, such mixed situations may be more common and equally valuable; however, they are rarely studied in the published literatures.

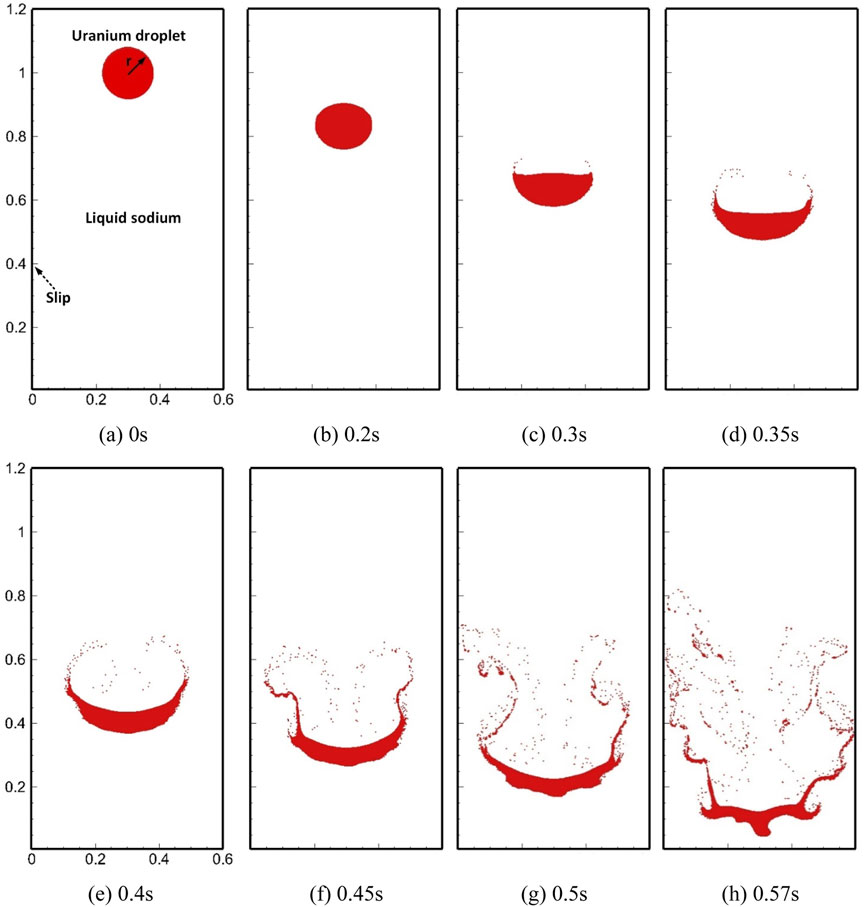
Regardless of heat transfer and phase transition, we assume that uranium, stainless steel, and sodium remain liquid and interact with each other. The hydrodynamic fragmentation in the FCI is our focus. The sodium pool is placed in a 2D Cartesian coordinate system with a width of 0.6 $m$ and height of 1.2 $m$. The uranium droplet, which has no initial velocity, with a radius of $r=$ 0.08 $m$ and with a center of (0.3, 1.0) is placed in the sodium pool. The computational domain is discretized into 450 × 900 particles. The timestep is set as $∆t={10}^{-5}s$. All the boundaries are considered free-slip. The gravity acceleration is g = 9.81 $m/s^2$. The density ratio between U, stainless steel (SS), and Na is 20:7.8:1 with ${\rho }_U=$ 17797 $kg/m^3$, ${\rho }_{SS}=$ 6920 $kg/m^3$, $\mathrm{a}\mathrm{n}\mathrm{d}{\rho }_{Na}=$ 892 $kg/m^3$. The other physical properties of the three materials used in this simulation are ${\eta }_U=$ 5.5 × 10^–3 $Pa\bullet s$, ${\alpha }_U$ =1.55 $N/m$, ${\eta }_{SS}=$ 5.36 × 10^–3 $Pa\bullet s$, ${\alpha }_{SS}$ =1.83 $N/m$, ${\eta }_{Na}=$ 4.067 × 10^–4 $Pa\bullet s$, and ${\alpha }_{Na}$ = 0.182 $N/m$. The artificial sound speeds are $c_U=40\sqrt{gH}$, $c_{SS}=32\sqrt{gH}$, and $c_{Na}=20\sqrt{gH}$. We first simulated the direct interaction between a single uranium droplet and sodium coolant. Then, the uranium droplet wrapped in stainless steel was further considered, and the thickness of the stainless steel film is set as 0.01 $m$ and 0.02 $m$. The thinner film thickness refers to the ratio of fuel cladding size to fuel pellet size in SFRs, which is 10% or slightly larger. The thicker film represents the condition that other stainless steel structures in the core also melt and participate in the FCI.

5.1 Breakup behavior

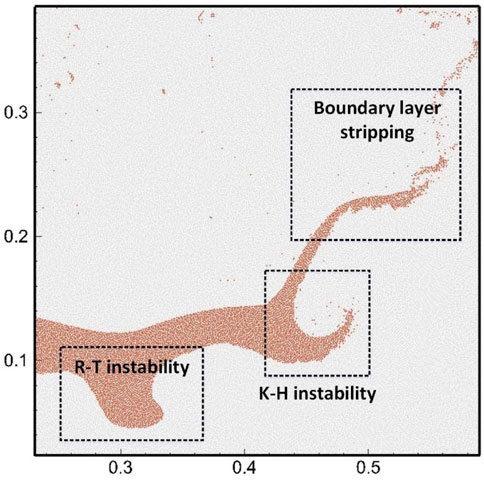
Figures 10, 11, 12 show the images of typical moments in the aforementioned three FCI processes, respectively. In order to clearly present the details of fragment distribution, we show uranium particles in red, stainless steel particles in green, and hide sodium particles. The simulated processes ended before liquid uranium hit the bottom of the sodium pool, which took about 0.57 s in all three cases. The initial layout for each case is shown in subfigure (a) of the series. In the process of direct interaction between uranium and sodium, as shown in Figure 10, the initially stationary uranium droplet began to slowly accelerate downward under gravity, and the circular droplet gradually developed into a crescent-shape droplet. Before 0.3 s, the droplet basically maintained good integrity. After that, the liquid sodium beneath the uranium droplet quickly flowed over the lower surface and carried a few small fragments away from the main body, rolling toward the low-pressure region behind the droplet and forming two vortexes, as shown in Figures 10D,E. As the falling speed of molten uranium increased, a large amount of uranium was elongated and stripped at the edge and is continuously taken away by the mainstream. The trailing vortices formed on both sides make the fragments more fully broken and dispersed in space. This is the typical phenomenon of boundary layer stripping. In addition, the main uranium body was obviously affected by Kelvin–Helmholtz (K–H) instability due to the relative velocity parallel to the interface and R–T instability due to gravity, both of which appeared later than the boundary layer stripping. Figure 13 shows the local magnified image at 0.57 s. The three hydraulic phenomena which are mentioned lead to the fragmentation which occurred simultaneously at that moment. They are in agreement with the discussion given by Nishimura et al. (2010) in form of a jet penetrating a surrounding fluid. Gray sodium particles are also shown in the magnified image included in Figure 13. We can observe that the complex interface can be clearly captured and particles near the interface with high density ratio are evenly distributed and accurately described. It proves the effectiveness of the KGC-MSPH method in solving FCI problems.

FIGURE 10. Initial setup and images in U-Na interaction.

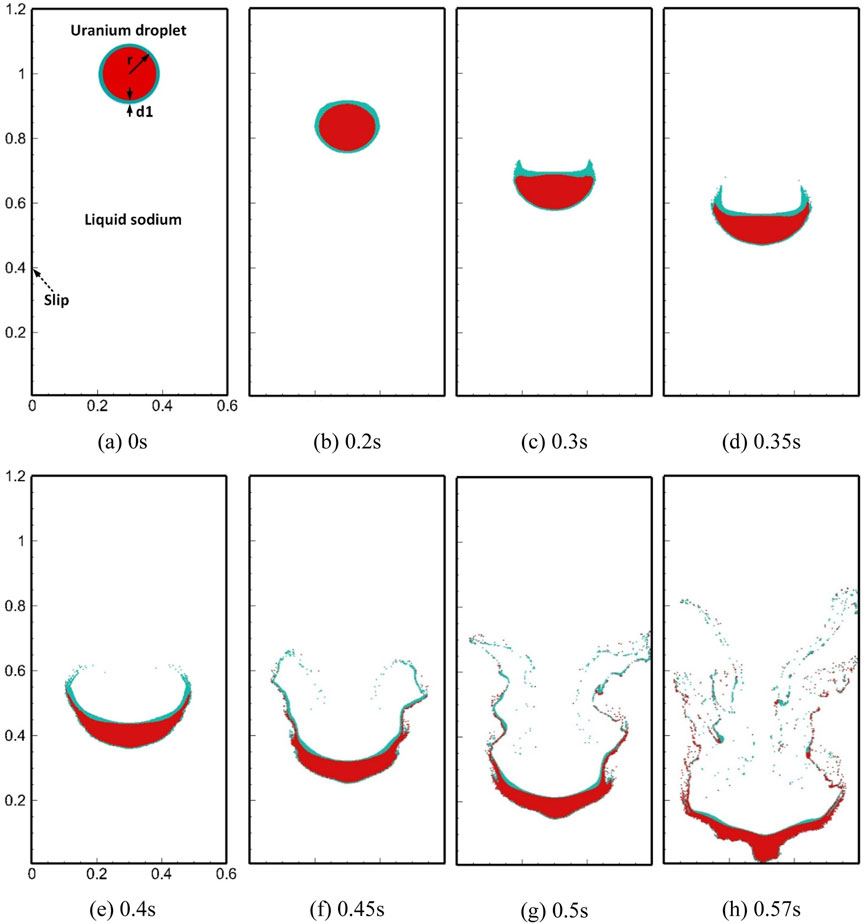
FIGURE 11. Initial setup and images in the interaction between U coated with Stainless steel film with thickness of 0.01 m and Na.

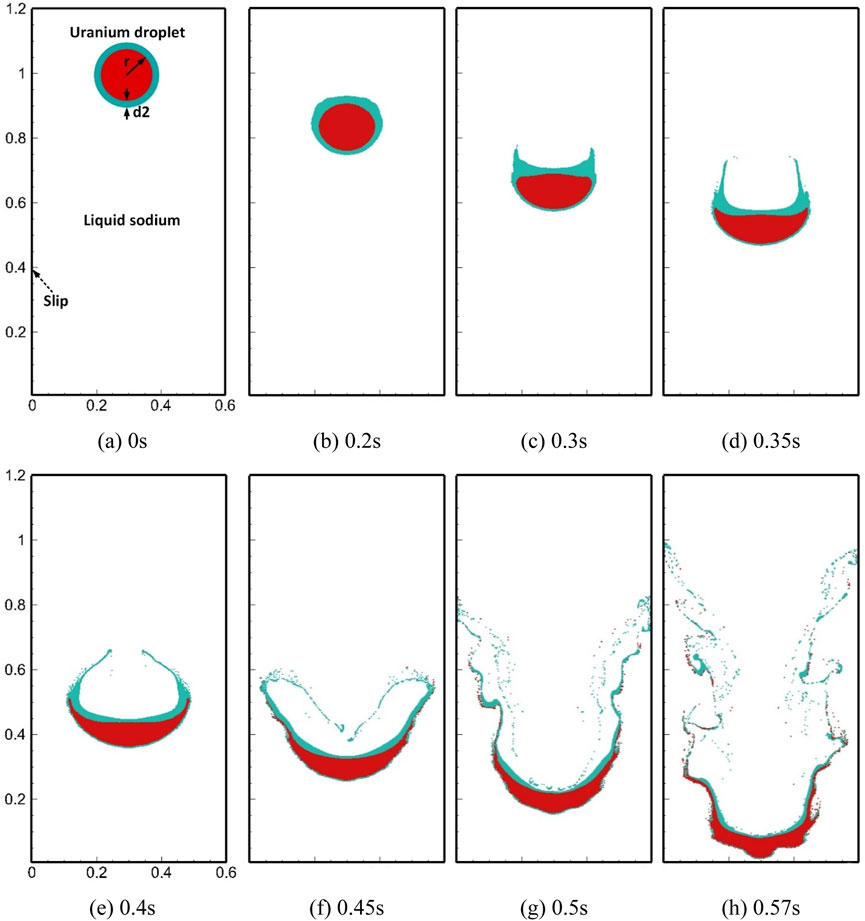
FIGURE 12. Initial setup and images in the interaction between U coated with Stainless steel film with thickness of 0.02 m and Na.

FIGURE 13. Local magnification in U-Na interaction at t = 0.57 s.

In the interactions between the uranium droplet coated with the stainless steel film and sodium coolant, the process can also be divided into two stages according to the integrity of the droplet. As shown in Figures 11, 12, the shape change of the uranium droplet in the first stage (0–0.35 s) is similar to that in the direct interaction and no fragments are generated. As mentioned previously, the dynamic viscosities of uranium and stainless steel are very close, and the density difference is not large, so the stainless steel film prevented the shear force from liquid sodium directly acting on the uranium surface. The isolation from the stainless steel film allowed the uranium droplets to remain unbroken for much longer than that in direct interaction, and the obtained droplet remained crescent-shaped. With falling speed, the lower stainless steel film gradually thinned under the shear forces and accumulated on the upper surface of the droplet. The stainless steel film was gradually elongated with the boundary layer movement and will be separated from the main body. In the later stage (0.35–0.57 s), the uranium at the crescent tips began to detach from the main body with the liquid stainless steel and formed uranium fragments which are adhered to stainless steel. The stainless steel film on the underlying surface of the main uranium body continued to be stretched and remained attached to the surface. The upper surface was always covered with a thicker film of stainless steel.

5.2 Result analysis

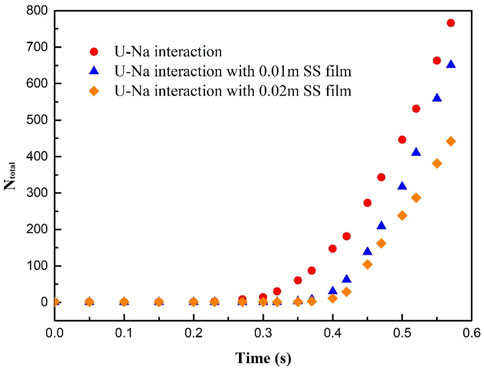
It can be observed from the FCI cases that the fragments formed mainly include a main uranium body with the largest mass and a large number of small fragments caused by boundary layer stripping. In order to illustrate the fragment distributions and analyze the influence of the stainless steel film, we made statistics on the total number of fragments and the mass change of the main uranium body. As shown in Figure 14, from the development trend of the total number of fragments, represented by $N_{total}$, it can be seen that the fragments in the direct U–Na interaction appeared earlier and were increasingly formed. We further analyzed the mass of the main body over time, as shown in Figure 15, expressed as the percentage of the mass of the main uranium body $\left(M_{\mathit{max}}\right)$ to the total uranium mass $\left(M_{total}\right)$. During the direct interaction, the mass detached from the main body is larger, resulting in the smallest mass of the final main body, about 73% of the total mass. In the other two cases, the mass of the main body is larger due to the isolation effect of the stainless steel film; the final mass fraction is 79% and 89%, respectively; and the interface deformation of the main body is less obvious and less easily broken.

FIGURE 14. The variation of total number of uranium fragments.

FIGURE 15. The variation of the mass fraction of the main uranium body relative to the total mass.

Therefore, according to the aforementioned simulation results, it can be concluded that the KGC-MSPH method can realize the simulation of multiphase flow with intense interface deformation under a large density ratio. The obtained interface is smooth, and the calculation is stable. In the 2D FCI simulation results, we can clearly observe the effect of boundary layer stripping, R–T instability and K–H instability. Boundary layer stripping is the main reason for the generation of small fragments, while R–T instability and K–H instability mainly cause the deformation of the main body. In addition to the direct interaction between uranium and sodium, we also considered the influence of the stainless steel film. The presence of the stainless steel film has a significant inhibition effect on uranium droplet fragmentation. The thicker the liquid film is, the more obvious the inhibition is, the smaller the number of fragments is, and the larger the size of the main body is. In addition, the obtained fragments of all sizes were adhered to stainless steel or wrapped by a thin stainless steel film. Our further analysis suggests that the hydraulic fragmentation of the molten fuel is impeded with the stainless steel film, and the larger debris produced is more likely to block coolant channels, leading to deterioration in core. On the other hand from the thermal perspective, the thermal conductivity of stainless steel is lower than that of uranium, and the stainless steel coat has a negative effect on the cooling of the molten fuel. The risk of re-criticality may arise, resulting in a pessimistic result. It is adverse to the safety of the reactor.

6 Conclusion

An improved MSPH with KGC is developed in this work to solve the simulation problem of multiphase flow with a large density ratio and drastic interface deformation. The KGC-MSPH is further applied to simulate FCI problems including the U–Na direct interaction and the interactions between uranium coated with stainless steel films of different thickness and sodium. The breakup behaviors, the number of fragments, and the mass of the main uranium body in each case are comparatively studied. The conclusions are drawn as follows:

1) Remarkable performance of KGC-MSPH is obtained; the unstable and mixed-interface problems are significantly solved. The capability of KGC-MSPH was validated by simulating the deformation of square droplet, R-T instability, and bubble rising in water.

2) Smoother interfaces can be obtained by considering the repulsive force model. The coefficient of this model applicable to this improved method is suggested to be around 0.01.

3) The breakup behaviors in all three FCI cases are similar, which are mainly affected by three hydraulic factors. Boundary layer stripping is the cause of the formation of a large number of small fragments. R–T instability and K–H instability act on the main body to deform the interface.

4) The stainless steel film can inhibit the breakup of the uranium droplet so that the integrity of the droplet can be maintained for a longer time, the number of fragments formed is less, and the main body size is larger. The thicker the liquid film is, the more obvious the inhibition effect is. The formed fragments and the main body are adhered to liquid stainless steel. The presence of the stainless steel film is suggested to be adverse to the safety of the reactor.

There are still some deficiencies in the simulation of FCI problems, which need to be improved in the future. The spatial scale of the sodium pool is limited, resulting in a short simulation process and the model is 2D. It can be further expanded in the computational domain scale and spatial dimension by solving the problem of computational cost. The thermal hydraulics behaviors closer to the actual situation can be simulated by further considering the thermodynamic model. With continuous development, the improved MSPH is expected to be a powerful tool for nuclear safety analysis and thermohydraulic calculation.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

FW carried out the method research and developed the code, performed the simulations, analyzed results, and wrote the manuscript. Z-GZ supervised the research and revised the manuscript. QW assisted in analyzing the results and writing the manuscript.

Funding

This research was supported by Projects of the National Natural Science Foundation of China [grant numbers 52176151 and 51476040], CNNC’s Pilot-innovation Research Project, and Fundamental Research Funds for the Central Universities of China [grant number 3072022TS1503].

Acknowledgments

The authors thank the projects for the financial support.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Nomenclature

Abbreviations

Symbols

$A$ Arbitrary function

$c$ Color function

$c_0$ Artificial sound speed (m/s)

$d$ Spatial dimension

${\mathit{f}}_w$ Repulsive force acceleration of wall (m/s²)

${\mathit{f}}_s$ Surface tension force (Kg/m²/s²)

${\mathit{f}}_v$ Viscous stress (Kg/m²/s²)

$\mathit{g}$ Gravity acceleration (m/s²)

$h$ Smoothing length (m)

$H$ Height (m)

$\mathit{I}$ Unit matrix

$i$ Center particle

$j$ Adjacent particle

$m$ Mass (kg)

$\mathit{n}$ Unit normal vector

$N$ Total number of particles

$p$ Pressure (Pa)

$p_b$ Background pressure (Pa)

$r$ Distance between two particles (m)

$R$ Radius (m)

$t$ Time (s)

$∆t$ Timestep (s)

$\mathit{v}$ Velocity vector (m/s)

$V$ Volume (m³)

$V^{\sigma }$ Special volume $\left({\mathrm{m}}^d\right)$

$W$ Kernel function $\left({\mathrm{m}}^{-d}\right)$

$\mathit{x}$ Position vector (m)

$∆x$ Uniform spacing (m)

Creek

$\alpha$ Surface tension coefficient (N/m)

$\gamma$ Stiffness parameter

$\kappa$ Curvature (m⁻¹)

$\lambda$ A density-weighted color function (m⁻¹)

$\eta$ Dynamic viscous coefficient (Pa·s)

$\epsilon$ Coefficient of repulsive force

$\rho$ Density (kg/m³)

${\rho }_0$ Reference density (kg/m³)

$\sigma$ Particle density number $\left({\mathrm{m}}^{-d}\right)$

$\upsilon$ Kinematic viscosity (m²/s)

$\Omega$ Volume of arbitrary domain (m³)

$\chi$ Interpolating function

$\Psi$ Density ratio

$\Phi$ Viscosity ratio